Zamów podręcznik wydawnicta MiGra (sklep wydawnictwa)
Reprezentacja danych w komputerze
Klas 3. Proponowany czas: 2 lekcjeLogiczny model komputera
Idea maszyny von Neumanna:- programy i dane posiadają taką samą postać
- programy i dane są przechowywane w tej samej pamięci
Uproszczony model komputera zgodny z ideą von Neumanna
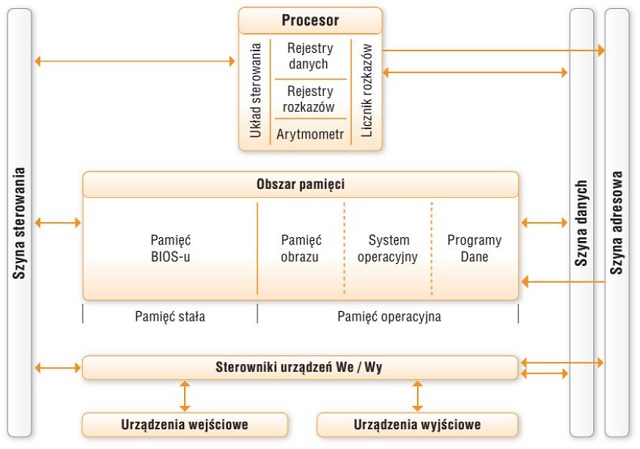
(źródło Informatyka dla szkół ponadpodstawowych Klasa 3 wyd. MiGra)
Działanie procesora
Procesor wykonuje operacje arytmetyczne i logiczne, odpowiada za prawidłową współprace wszystkich modułów funkcjonalnych komputera. Zbiór operacji arytmetyczno- logicznych tworzy listę rozkazów procesora.
Ze względów technicznych rozkazy procesora oparte są na sygnale elektrycznym, który może przyjąć tylko dwa stany: jest napięcie, nie ma napięcia elektrycznego. Przyjmuje się, że obecność sygnału odpowiada cyfrze 1, a brak sygnału- cyfrze 0.
Każda z wartości 0 lub 1 stanowi jeden bit informacji. Kombinacja zer i jedynek tworzy matematyczny zapis dowolnej liczby w systemie dwójkowym. Ciąg ośmiu bitów jest bajtem
1 B (bajt)= 8 b (bit)Przykład przeliczników wielkości jednostek pamięci
- 1 Kb = 1024 b
- 1 Mb = 1024 Kb
- 1 KB = 1024 B
- 1 MB = 1024 KB
Ciąg bitów
Ciąg bitów nazywamy binarnym rozwinięciem liczby
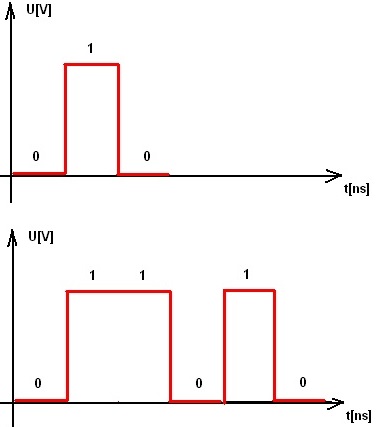
Najbardziej znaczący bit stoi z lewej strony a najmniej z prawej strony rozwinięcia
System pozycyjny
System pozycyjny, to taki sposób reprezentowania liczby, w którym wartość liczby zależy od pozycji cyfry w ciągu cyfr.
Liczba zapisana w dowolnym systemie pozycyjnym
an-1 an-2... a1a0gdzie n, to ilość cyfr tworzących daną liczbę
Rozwinięcie dowolnej liczby zapisuje się według poniższego wzoru
an-1⋅pn-1+ an-2⋅pn-2+...+ a1⋅p1+ a0⋅p0gdzie p, to podstawa systemu
Przykład rozwinięcia liczby dziesiętnej
532=5⋅100+3⋅10+2⋅1=5⋅102+3⋅101+2⋅100Jak odczytać wartość liczby zapisanej w systemie dwójkowym?
Aby obliczyć wartość dziesiętną liczby zapisanej w systemie dwójkowym korzystamy ze wzoru na rozwinięcie, w którym podstawą systemu jest liczba 2 ( w systemie trójkowy jest 3 itd)
Liczba 101011(2)=?(10)
1⋅25+0⋅24+1⋅23+0⋅22+1⋅21+1⋅20=25+23+21+20=32+8+2+1=43Wyznaczenie rozwinięcia dwójkowego liczby dziesiętnej
Chcąc zapisać liczbę z systemu dziesiętnego na przykład w systemie dwójkowym (binarnym) wykonujemy dzielenie z resztą tej liczby przez dwa (podstawę systemu docelowego), zapisujemy wszystkie reszt z dzieleń do momentu otrzymania ilorazu równego zero. Wynikiem jest odczyt od końca kolejnych reszt.
Na przykład: jakie jest rozwinięcie binarne liczby dziesiętnej 749(10)=?(2)
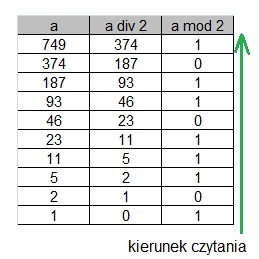
749(10) = 1011101101(2)
System szesnastkowy
System szesnastkowy oprócz cyfr zawiera symbole pierwszych sześciu wielkich liter alfabetu, czyli A, B, C, D, E i F. Symbole te odpowiednio odpowiadają wartościom 10, 11, 12, 13, 14, 15.
Przykładowo liczba szesnastkowa 4AD(16) w systemie dziesiętnym odpowiada wartości:
4AD(16)=4⋅162+A⋅161+D⋅160=4⋅162+10⋅161+13⋅160=4⋅256+10⋅16+13⋅1=1197(10)Wyznaczanie rozwinięcia szesnastkowego liczby dziesiętnej
Wyznaczanie rozwinięcia szesnastkowego liczby dziesiętnej odbywa się na tych samych zasadach co rozwinięcia binarnego liczby dziesiętnej z tą różnicą, że podstawą jest liczba 16.
Chcąc zapisać liczbę z systemu dziesiętnego w systemie szesnastkowym wykonujemy dzielenie z resztą tej liczby przez 16 (podstawę systemu docelowego), zapisujemy wszystkie reszt z dzieleń do momentu otrzymania ilorazu równego zero. Każdą z reszt większą od 9 zamieniamy na odpowiedni symbol literowy. Wynikiem jest odczyt od końca kolejnych reszt.
Na przykład: jakie jest rozwinięcie szesnastkowe liczby dziesiętnej 749(10) ?
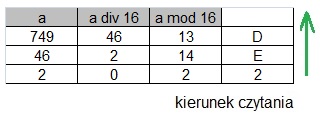749(10) = 2ED(16)
