Algorytm badania pierwszości liczb

Liczba pierwsza to liczba naturalna większa od 1, która ma tylko dwa dzielniki naturalne: jedynkę i samą siebie. Przykład kilku liczb pierwszych to: 2, 3, 5, 7, 11, 13

Aby sprawdzić czy podana liczba jest pierwsza, to należy wyszukać wszystkie jej dzielniki większe od 1 i mniejsze od niej samej. Jeżeli się takich nie znajdzie, to znaczy, że badana liczba jest liczbą pierwszą.

Realizacja takiego algorytmu będzie polegać na wykonaniu pętli szukania reszty z dzielenia dla kolejnych kandydatów na dzielniki. Znalezienie dzielnika (czyli reszta z dzielenia wynosi 0) oznacza, że dana liczba nie jest liczbą pierwszą.

Zakres przeszukiwania można zmniejszyć (co przyspiesza działanie algorytmu), jeżeli górną granicę określimy na wartość pierwiastka kwadratowego z badanej liczby. Wynik pierwiastkowania zaokrąglamy w dół.

Schemat algorytmu sprawdzającego czy podana liczba jest liczbą pierwszą

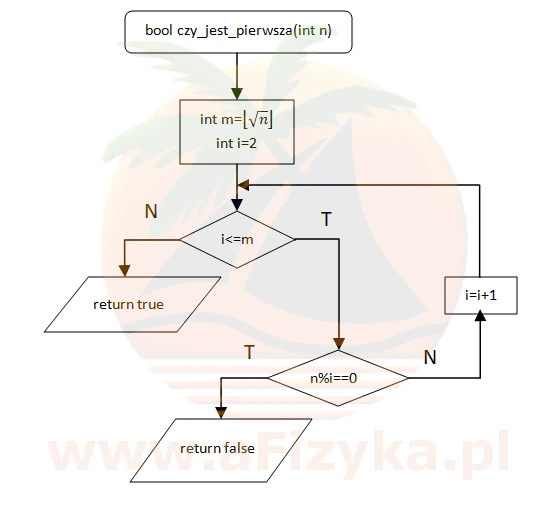
Algorytm badania pierwszości liczb. Visual studio C#

Ciało funkcji realizującej powyższy algorytm (język C#)

Wskazówka:


private bool czy_jest_pierwsza(int n)
        {
            int m = (int)Math.Floor(Math.Sqrt(n));
            for (int i = 2; i <= m; i++)
                if (n % i == 0) return false;//nie jest pierwszą
            //jest pierwszą
            return true;
        }

Przykładowa aplikacja badająca pierwszość liczb napisana w Visual Studio

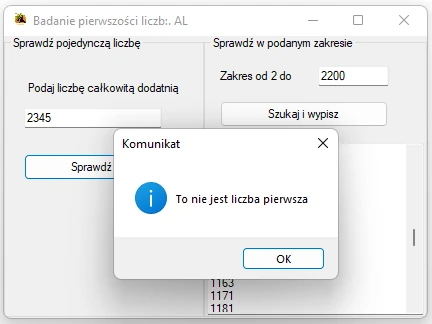
aplikacja badania pierwszości liczb. Visual studio C#

Pełny kod pliku klasy Form utworzonej formatki aplikacji

Form1.cs


using System;
using System.Collections.Generic;
using System.ComponentModel;
using System.Data;
using System.Drawing;
using System.Linq;
using System.Text;
using System.Threading.Tasks;
using System.Windows.Forms;

namespace _2AlgCzyLiczbaJestPierwsz
{
    public partial class Form1 : Form
    {
        private bool czy_jest_pierwsza(int n)
        {
            int m = (int)Math.Floor(Math.Sqrt(n));
            for (int i = 2; i <= m; i++)
                if (n % i == 0) return false;//nie jest pierwszą
            //jest pierwszą
            return true;
        }

        public Form1()
        {
            InitializeComponent();
        }

        private void textBox1_KeyPress(object sender, KeyPressEventArgs e)
        {
            //zabezpiecz przed znakami nienumerycznymi
            if (e.KeyChar == 8) return;//wyskocz jak BackSpace
            if (e.KeyChar < '0' || e.KeyChar > '9') e.Handled = true;
        }

        private void button1_Click(object sender, EventArgs e)
        {
            if (textBox1.Text.Length < 1) return;
            int liczba=Int32.Parse(textBox1.Text);
            if (czy_jest_pierwsza(liczba))
                MessageBox.Show("To jest liczba pierwsza",
                                "Komunikat",
                                MessageBoxButtons.OK,
                                MessageBoxIcon.Information);
            else
                MessageBox.Show("To nie jest liczba pierwsza",
                "Komunikat",
                MessageBoxButtons.OK,
                MessageBoxIcon.Information);
        }

        private void button2_Click(object sender, EventArgs e)
        {
            //wyskocz bo nie podano górnego zakresu
            if (textBox2.Text.Length < 1) return;
            textBox3.Clear();
            int i= 2,k= Int32.Parse(textBox2.Text);
            while (i < k)
            {
                if (czy_jest_pierwsza(i))
                    textBox3.AppendText(i.ToString()+Environment.NewLine);
                i++;
            }
        }
    }
}

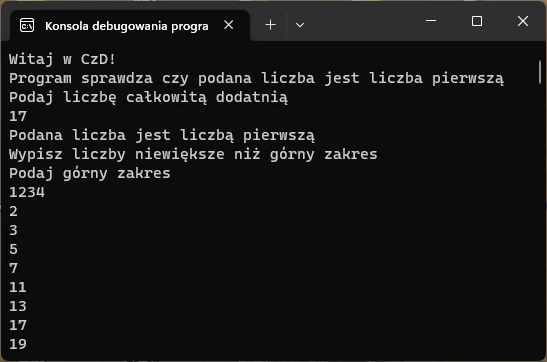
Rozwiązanie w C# pod konsolę

Wynik działania programu

Algorytm badania pierwszości liczb kod pod konsolę. Visual studio C#

Kod programu

Wskazówka:

 
using System;

namespace _2AlgCzyLiczbaJestPierwsz_c_h
{
    class Program
    {
        static bool czy_jest_pierwsza(int n)
        {
            int m = (int)Math.Floor(Math.Sqrt(n));
            for (int i = 2; i <= m; i++)
                if (n % i == 0) return false;
            return true;
        }

        static void Main(string[] args)
        {
            Console.WriteLine("Witaj w CzD!");
            Console.WriteLine("Program sprawdza czy podana liczba jest liczba pierwszą");
            Console.WriteLine("Podaj liczbę całkowitą dodatnią");
            int liczba= Convert.ToInt16(Console.ReadLine());
            if (czy_jest_pierwsza(liczba))
                Console.WriteLine("Podana liczba jest liczbą pierwszą");
            else
                Console.WriteLine("Podana liczba nie jest liczbą pierwszą");
            Console.WriteLine("Wypisz liczby niewiększe niż górny zakres");
            Console.WriteLine("Podaj górny zakres");
            int granica = Convert.ToInt16(Console.ReadLine());
            int i = 2;
            while (i <= granica)
            {
                if(czy_jest_pierwsza(i))
                   Console.WriteLine(i);
                i++;
            }
        }
    }
}

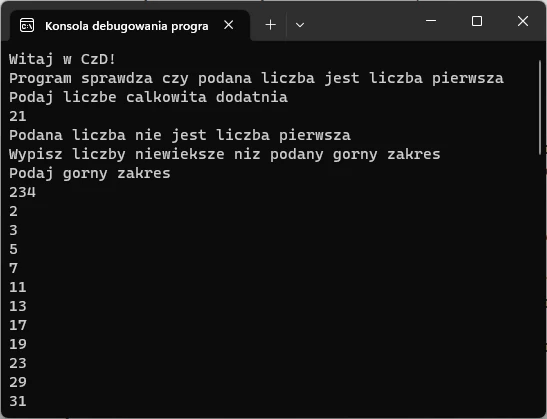
Rozwiązanie C++ kod pod konsolę

Wynik działania programu

Algorytm badania pierwszości liczb kod pod konsolę kod c++

Kod programu

Wskazówka:


#include <iostream>
#include <string.h>
#include <cmath>
using namespace std;

bool czy_jest_pierwsza(int n) {
    int m = floor(sqrt(n));
    for (int i = 2; i <=m; i++)
        if (n % i == 0)return false;
    return true;
}

int main()
{
    cout << "Witaj w CzD!\n";
    cout << "Program sprawdza czy podana liczba jest liczba pierwsza\n";
    cout << "Podaj liczbe calkowita dodatnia\n";
    int liczba;
    cin >> liczba;
    if (czy_jest_pierwsza(liczba))
        cout << "Podana liczba jest liczba pierwsza\n";
    else
        cout << "Podana liczba nie jest liczba pierwsza\n";
    cout << "Wypisz liczby niewieksze niz podany gorny zakres\n";
    cout << "Podaj gorny zakres\n";
    int granica;
    cin >> granica;
    int i = 2;
    while (i <= granica) {
        if (czy_jest_pierwsza(i))
            cout << i << endl;
        i++;
    }
}