Pewien narciarz, stojąc na szczycie góry, postanowił pobić swój rekord w zjeździe...Zbiór zadań wielopoziomowych z fizyki 7-8 wyd. WSiP

Rozwiązanie zadania:

Odp. 1 Obliczamy czas zjazdu narciarza

Skorzystamy ze wzoru na drogę w ruchu jednostajnie przyspieszonym, z którego po przekształceniu obliczymy szukany czas

Odp. Szukany czas zjazdu wynosi 8 sekund

Odp. 2 Obliczamy szybkość narciarza u podnóża góry

Skorzystamy z definicji przyspieszenia, z której po przekształceniu obliczymy szukaną szybkość narciarza

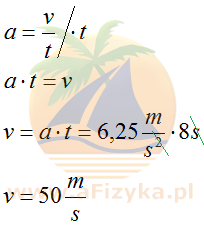
Odp. Szybkość narciarza u podnóża góry wynosi 50m/s

Odp. 3 Obliczamy średnią szybkość narciarza

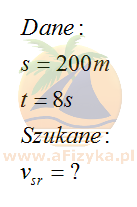
Szybkość średnia jest równa ilorazowi przebytej drogi przez czas potrzebny na pokonanie tej drogi

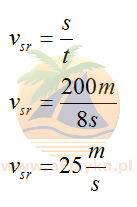
Odp. Szybkość średnia narciarza wynosi 25m/s

Odp. 4 Rysujemy wykres zależności szybkości narciarza od czasu

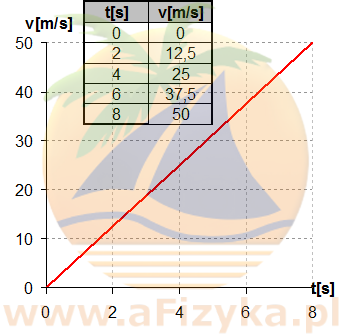
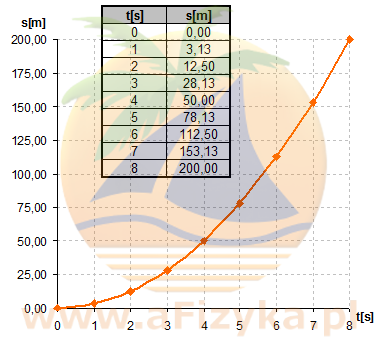
Odp. 5 Rysujemy wykres zależności przebytej drogi przez narciarza od czasu

Odp. 6 Obliczamy, o ile musiałby być dłuższy stok, aby zjazd trwał o 2 sekundy dłużej

Wskazówka: Z poprzednich obliczeń wiemy, że czas jazdy na stoku o długości 200m wynosi 8 sekund. Z nowych warunków zadania wynika, ze narciarz musi jechać o 2 sekundy dłużej, czyli 10 sekund z tym samym przyspieszeniem 6,25m/s²

Obliczamy jaką drogę pokona narciarz w czasie 10 sekund

Obliczamy szukaną różnicę dróg Δs

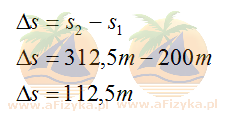
Odp. Stok musiałby być dłuższy o 112,5m