Cytat: Proton i jądro helu (składające się z dwóch protonów i dwóch neutronów) poruszają się w polu elektrostatycznym miedzy dwoma punktami A i B ... Świat Fizyki podręcznik dla uczniów gimnazjum, część 3
Przedstawiona treść zadania jest tylko fragmentem (cytatem) całej treści zamieszczonej w podręczniku lub zbiorze zadań. Aby w pełni można było skorzystać z analizy rozwiązania zadania, należy znać pełną treść zadania. Zachęcamy do kupna danego podręcznika lub zbioru zadań z fizyki.
Rozwiązanie wybranego zadania:
Kliknij aby zobaczyć inne rozwiązania
Zapiszemy dane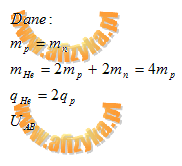
Odp. a) Szukamy jaką pracę wykonuje pole nad jądrem heli oraz protonem
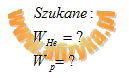
Obliczamy prace jaką pole elektrostatyczne wykona nad protonem i jądrem helu przesuwając je z punktu A do B. Korzystamy z zależności na napięcie w polu elektrostatycznym
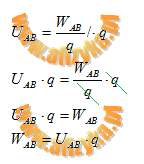
dla protonu wartość pracy wynosi
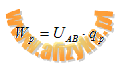
dla jądra helu wartość pracy wynosi
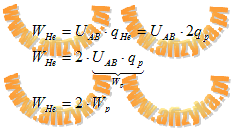
Odp. Pole elektrostatyczne wykona dwukrotnie większą pracę nad jądrem helu niż nad protonem
Odp. b) Obliczamy szybkość protonu i jądra helu uzyskaną między punktami A i B:
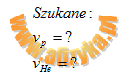
Praca siły elektrostatycznej nad protonem i jądrem helu w czasie przesunięcia równa jest przyrostowi energii kinetycznej obu ciał (wynika to z zasady zachowania energii). Uwaga: w punkcie początkowym (A) oba ciała spoczywały, więc ich energie kinetyczne wynosiły zero.
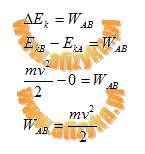
Przekształcamy otrzymaną zależność tak, aby otrzymać wzór na szybkość (v)
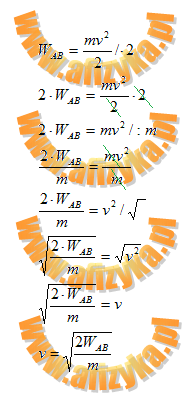
Po uwzględnieniu zależności
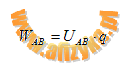
otrzymujemy:
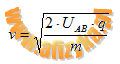
-dla protonu
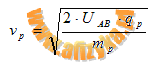
-dla jądra helu
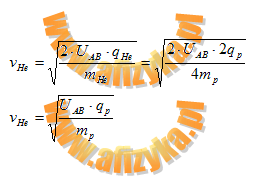
Porównujemy obie szybkości przez obliczenie ich stosunku
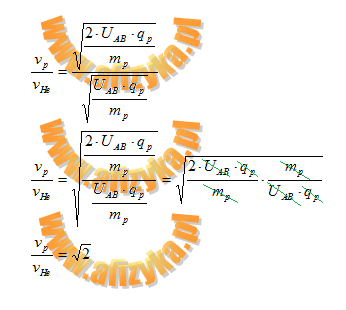
Odp. Prędkość protonu jest pierwiastek z dwóch razy większa od prędkości jądra helu
Odp. c) Obliczamy, która z cząstek uzyska większy pęd:
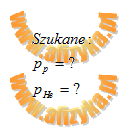
Z definicji pędu możemy zapisać wzór:
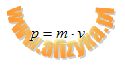
- dla protonu
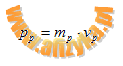
- dla jądra helu:
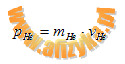
po uwzględnieniu że:
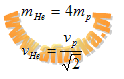
otrzymujemy:
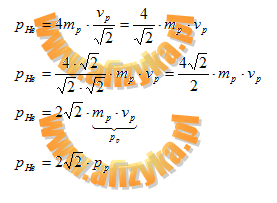
Odp. Pęd jądra helu jest dwa razy pierwiastek z dwóch razy większy od pędu protonu.
Odp. d) Wyznaczamy przyspieszenia obu cząstek korzystając z II zasady dynamiki Newtona
Szukane:
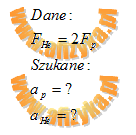
Na podstawie II zasady Newtona, zapiszemy wzorem przyspieszenie
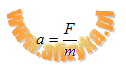
- dla protonu
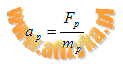
- dla jądra helu
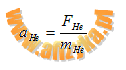
Po uwzględnieniu
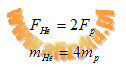
otrzymujemy:
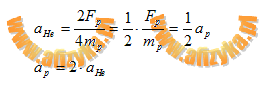
Odp. Przyspieszenie protonu jest dwukrotnie większe od przyspieszenia jądra helu.
Odp. e) Wyznaczamy czas przebycia odcinka AB przez obie cząstki
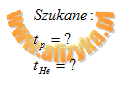
Aby wyznaczyć czas w jakim każda z cząstek pokona odcinek AB skorzystamy z definicji przyspieszenia
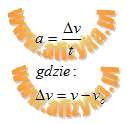
szybkość początkowa vo wynosi zero, czyli
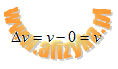
Przekształcamy wzór na przyspieszenie tak, aby wyznaczyć czas (t)
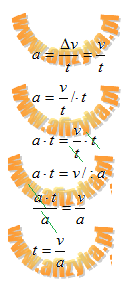
- czas dla jądra helu

- czas dla protonu
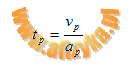
po uwzględnieniu że:
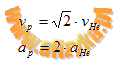
otrzymamy
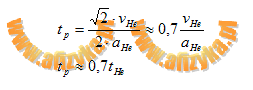
Odp. Odcinek AB w krótszym czasie przebywa proton.

 Zobacz przepis na wyśmienite gofry
Zobacz przepis na wyśmienite gofry